Целью данной работы является исследование сигнала - радиоимпульса специальной формы. Задача состоит в комплексном подходе к проведению анализа, и включает в себя как математические расчёты с пояснениями, так и описание сигнала и области его применения.
1. Задание
Для анализа в данной работе взят следующий сигнал (далее для анализа используется MathCAD 2001):
|
(1) |
|
(2) |
Для определённости построения графиков и оценки величин:
|
(3) |
Нужно:
- Дать описание сигнала, изобразить временную диаграмму сигнала
- Получить выражение для комплексной спектральной плотности и получить выражения и изобразить частотные зависимости модуля и аргумента комплексной спектральной плотности
- Получить выражение и привести график энергетического спектра сигнала
- Определить энергию сигнала
- Найти выражение и привести график автокорреляционной функции сигнала
- Качественно оценить влияние изменения параметров сигнала.
2. Описание сигнала
Из выражения функции сигнала видно, что он представляет собой радиоимпульс с колоколообразной мадулирующей функцией. Т.е. имеет место амплитудная модуляция. Модулирующая функция представляет собой т.н. гауссов импульс, который уникален тем, что он сам и его спектр
выражаются одинаковыми функциями и обладают свойством симметрии: для получения одной из
них по заданной другой достаточно заменить t на (см. [1], Гл.2, §9, с. 54).
Заполнение - косинус, гармоническая функция. Наиболее часто в качестве несущей модулируемой функции берется именно синусоидальная функция (синус или косинус, определяется вобщем-то начальной фазой), т.к. её просто получать и удобно использовать.
Построим для начала график функции сигнала и его модулирующую функцию:
Рис.1 Временная диаграмма исследуемого сигнала
Как известно (см. [3], Гл.3, §3, c. 140-145), колоколообразный импульс имеет сравнительно узкую ширину полосы излучения (ШПИ) при большой скорости убывания спектра. Это даёт возможность передачи сигнала в узкой полосе частот (т.е. при такой АМ на частотах, значительно отличающихся от несущей излучение будет очень малым). А значит такие сигналы могут применяться в многоканальных системах передачи.
3. Комплексная спектральная плотность
Для получения выражения комплексной спектральной плотности используем свойство преобразования Фурье, а именно смещение спектра колебания. Т.к. умножение функции s(t) на гармоническое колебание эквивалентно расщеплению спектра S(w) на две части (см. [1], Гл.2, §7, c. 45):
(4) В качестве s(t) у нас модулирующая функция U(t). Поэтому для начала найдём её комплексную спектральную плотность:
(5)Для вычисления интеграла удобно в подинтегральной функции дополнить показатель степени до квадрата суммы:
Таким образом, выражение (5) можно привести к виду:
Вводя новую переменную x=(t/ti)+d (dt=ti*dx) получаем:
Интеграл, входящий в выражение является табличным (см. [4], Отдел 6, §1, с. 563) и равен , тогда:
(6)Тогда, используя (4), получаем:
(7)Для построения графика спектральной плотности гауссова импульса (модулирующего) используем MathCAD. Проверим, правильно ли рассчитана спектральная плотность построением графика, полученного прямым интегрированием
Рис.2 Спектральная плотность модурирующего импульса.
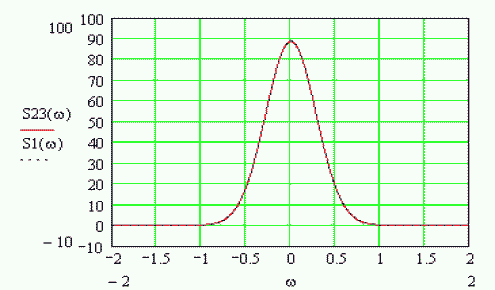
Видно, что графики совпали, что подтверждает расчёты, также видно, что спектральная плотность модулирующего импульса не является комплексным числом.
Пределы интеграла не бесконечны ввиду ограниченных возможностей MathCAD и моей вычислительной системы, но вполне достаточны для построения графика. Модуль комплексной спектральной плотности (7), вычислим следующим образом: прибегнем к геометрической интерпретации в комплексной плоскости, воспользовавшись тем, что спектральные плотности модулирующей функции действительные, а потом проверим точность выражения с помощью MathCAD. Итак, приводим для наглядности здесь ещё раз формулу (7):
(7)Представляя спектральную плотность в виде комплексной амплитуды:
Рис. 3 Представление спектральной плотности в виде комплексной амплитуды
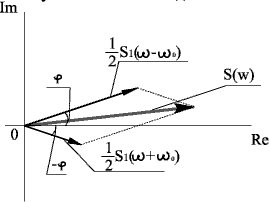
Модуль комплексной спектральной плотности, как видно из этой интерпретации будет равен длине вектора S(w). Воспользовавшись выражением, известным из геометрии (см. [4], Отдел 2, Гл.4, §3, с.185), получаем:
(8)Строя на одном функциональном графике модуль из выражения (7) и полученный нами с помощью геометрической интерпретации, убеждаемся, что они совпадают, а значит интерпретация справедлива:
Рис. 4 Модуль спектральной плотности исследуемого сигнала
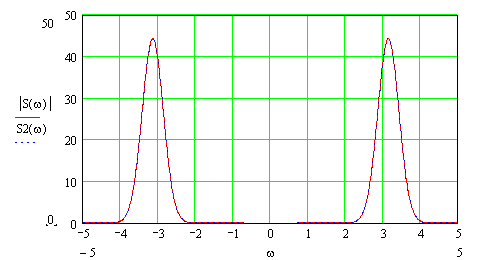
Как и следовало ожидать, максимумы находятся на частотах ±w0, и амплитуды вдвое уменьшились. Упрощая (8), получим аналитическое выражение для модуля спектральной плотности, имеем:
Для нахождения аргумента спектральной плотности воспользуемся тем же геометрическим представлением (см. Рис.3), а зависимость фазы, найдётся тогда как арктангенс (см. [4], Отдел 2, Гл.4, §3, с.185):
Рис.5 Аргумент комплексной спектральной плотности (фазо-частотный спектр)
Видно, что фаза меняется от -ф до +ф. Если бы начальная фаза ф отсутствовала, то фаза бы всюду была равна 0, как у гауссова импульса без косинусоидального заполнения.
4. Энергетический спектр сигнала
Собственный энергетический спектр сигнала найдём как квадрат модуля комплексной спектральной плотности (9):
(11)
Рис.6 Энергетический спектр исследуемого сигнала
Видно, что энергия сосредоточена в узком интервале частот, что и позволяет использовать
подобные импульсы при многоканальной связи.
Энергию же сигнала найдём как
, или, т.к. модуль спектральной плотности симметричен относительно ω=0 рад. так:
5. Автокорреляционная функция (АКФ) сигнала
Как известно автокорреляционная функция является чётной функцией t (t - временной сдвиг относительно самой себе). При t=0 она равна энергии сигнала Es, итак, имеем:
Рис.7 График автокорреляционной функции сигнала
Как видно из графика огибающая АКФ имеет форму, схожую с огибающей самого радиоимпульса.
6. Оценка влияния параметров сигнала на его спектральную плотность и АКФ
Изменение начальной фазы не отразится на изменении модуля спектральной плотности (т.к. он связан с амплитудой) и не повлияет на АКФ, т.к. та является заведомо чётной, и, кроме того, может быть найдена как
Изменение начальной фазы повлияет на ФЧС, т.е. на аргумент комплексной спектральной плотности. Например поменяв начальную фазу с π/8 на π/4, обнаруживаем что фаза теперь будет меняться в пределах: -π/4 до +π/4.
Рис.8 Изменение ФЧС связано с изменением начальной фазы
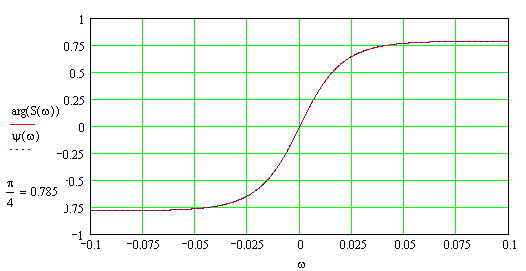
Если начальная фаза будет отрицательной, то соответственно изменится и график ФЧС: теперь это функция монотонно убывающая
Рис.9 ФЧС при отрицательной начальной фазе, равной -π/4
Изменение амплитуды A в 2 раза, напротив, не ведёт к изменению ФЧС, зато ведёт к уменьшению в 2 раза мгновенных амплитуд модуля спектрольной плотности, и уменьшению в 4 раза мгновенных амплитуд энергетического спектра и АКФ:
Рис.10 Изменение модуля спектральной плотности и амплитуды АКФ
связано с амплитудой сигнала
Увеличение в 2 раза параметра ti, связанного с временем нарастания и спада огибающей радиоимпульса приводит к растяжению сигнала во времени: его огибающая становится более пологой, как известно это ведёт к сужению спектра: амплитуда модуля комплексной спектральной плотности в точках своего максимума становится в два раза больше, но вдвое меньше становится ШПИ (ширина полосы излучения). Фаза также теперь меняется быстрее. Огибающая АКФ, по форме осталась той же, но амплитуда выросла в 2 раза, и огибающая растянулась во времени, как и сигнал, в 2 раза. Уменьшение же параметра ti, напротив, приводит к сужению сигнала во времени, расширению спектра, падению амплитуды АКФ и сужению во времени её огибающей.
Рис. 11 Изменения в АЧС, ФЧС и изменения автокорреляционной функции, связанные с
увеличением параметра ti в 2 раза
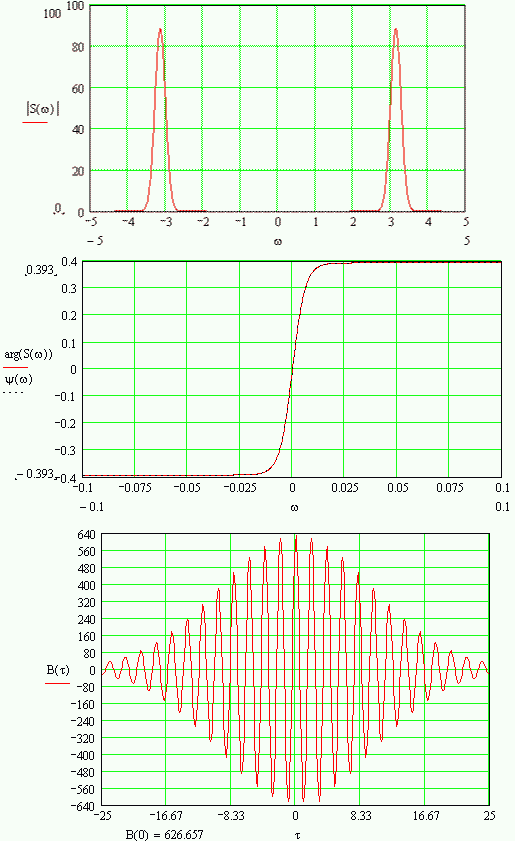
Увеличение в 2 раза несущей частоты ω0 приведёт к разносу двух составляющих модуля спектральной плотности: как известно максимумы находятся на частотах ω0. ФЧС не изменится, а АКФ не изменит форму огибающей, но колебаться будет, как и сигнал, в 2 раза быстрее:
Рис. 12 Изменения в АЧС, и изменения корреляционной функции, связанные с
увеличением несущей частоты в 2 раза
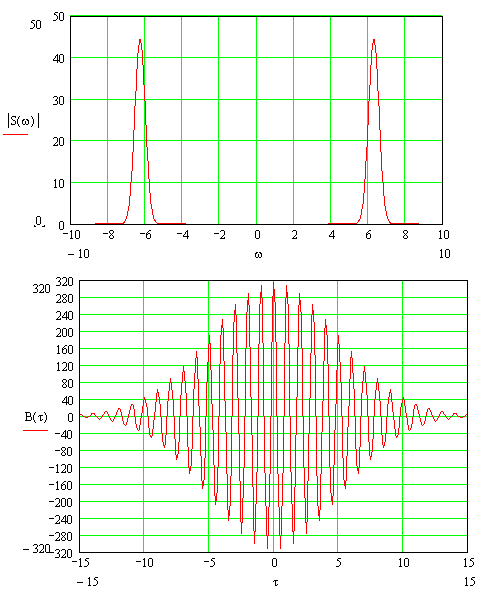
Вывод: в ходе работы был проведён анализ сигнала с использованием комплексного подхода, были вычислены комплексная спектральная плотность, АЧС, ФЧС, автокорреляционная функция, энергетический спектр, энергия сигнала, даны качественные оценки влияния изменения параметров сигнала на его спектральную плотность и корреляционную функцию.
Литература:
1. И.С. Гоноровский. Радиотехнические цепи и сигналы. Учебник для вузов. М., "Сов. Радио", 1977 2. С.И. Баскаков. Радиотехнические цепи и сигналы. Учебник для вузов. М., "Высшая школа", 2000 3. Ю.Л. Комиссаров, С.С. Родионов. Помехоустойчивость и электромагнитная совместимость радиоэлектронных средств. Киев, "Технiка", 1978 4. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся втузов. М., "Наука", 1965