Цель работы:

Используя быстрое преобразование Фурье, найти дискретный спектр сигнала.

 Для выполнения этой работы будем использовать заслуженно популярную программу для работы с числовыми данными SciLab. Программа является свободно распространяемой, в отличие от, также мощной, но коммерческой, среды MATLAB.

SciLab регулярно обновляется. Текущая версия программы: 5.4.1.

Построение АЧХ и ФЧХ

 Считываем wav - файл варианта в массив, получая глубину оцифровки (в битах) и частоту дискретизации сигнала

 [y,Fs,bits]=wavread("N1 V3.wav");Fs,bits

Fs =
44100.  

bits =
16.  

Размер массива y составляет: 220397
Построим временную диаграмму сигнала:

  Рисунок 1 Временная диаграмма сигнала

Результат – количество спектральных (комплексных) отсчётов соответствует изначальному количеству временных отсчётов.

Для того, чтобы провести быстрое преобразование Фурье по классическому алгоритму, необходимо дополнить количество отсчётов до 2^N нулями, ближайшим является 262144, либо сократить выборку до 2^N в меньшую сторону, если разрешение по частотным составляющим будет нас устраивать. Возьмём 2¹⁷ = 131072 отсчёта для построения спектра.

Сделаем быстрое преобразование Фурье:
-->Y=fft(y(1: 131072));
Спектральные отсчёты АЧС являются зеркальными:
АЧС:
-->plot(abs(Y));
Добавим сетку:
-->xgrid(100);

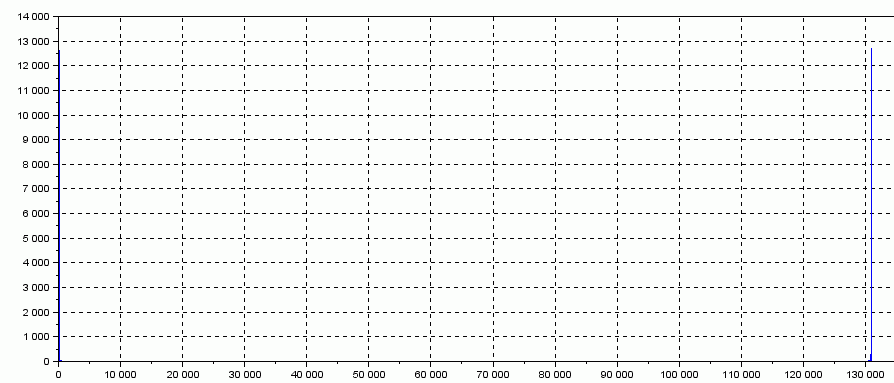
Рисунок 2 Амплитудно-частотный спектр (AЧС)

Фазовый спектр:

-->Y=fft(y(1:131072));
-->Phz = atan(imag(Y),real(Y));
-->plot(Phz);
-->xgrid(100);

Рисунок 3 Фазо-частотный спектр (ФЧС)

Амплитудные спектральные составляющие сосредоточены вблизи нулевой частоты, т.е. спектр относительно низкочастотный.

Посмотрим амплитудный и частотный спектры в области низких частот и приведём ось х к частотам (частота дискретизации 44000 Гц).

Частоты АЧС, начиная с нулевой:

Fn = 0, Fs/N, 2*Fs/n… Fs/2-1.

-->frq=Fs/(2^17):Fs/(2^17):Fs/2;
-->clf(); % очитим экран
-->plot(frq(1:250),abs(Y(1:250))); %отобразим график
-->xgrid(100); %сетка

 Рисунок 4 Приближение АЧС, внизу - частоты (Гц)

 -->clf();
-->plot(frq(1:250),Phz(1:250));
-->xgrid(100);

 Рисунок 5 Приближение ФЧС, внизу - частоты (Гц)

Приведение амплитуды сложнее, т.к. частота семплирования не кратна частотам сигнала и имеет место размывание спектра.

Для уменьшения этого эффекта (искажение амплитуды в этом случае – это т.н. “эффект частокола”) используем оконную функцию Flat Top.

Создадим окно при помощи библиотеки tftb_window.sci

-->H=tftb_window(2^17,'FlatTop');
-->clf();
-->plot(H);
-->xgrid(100);

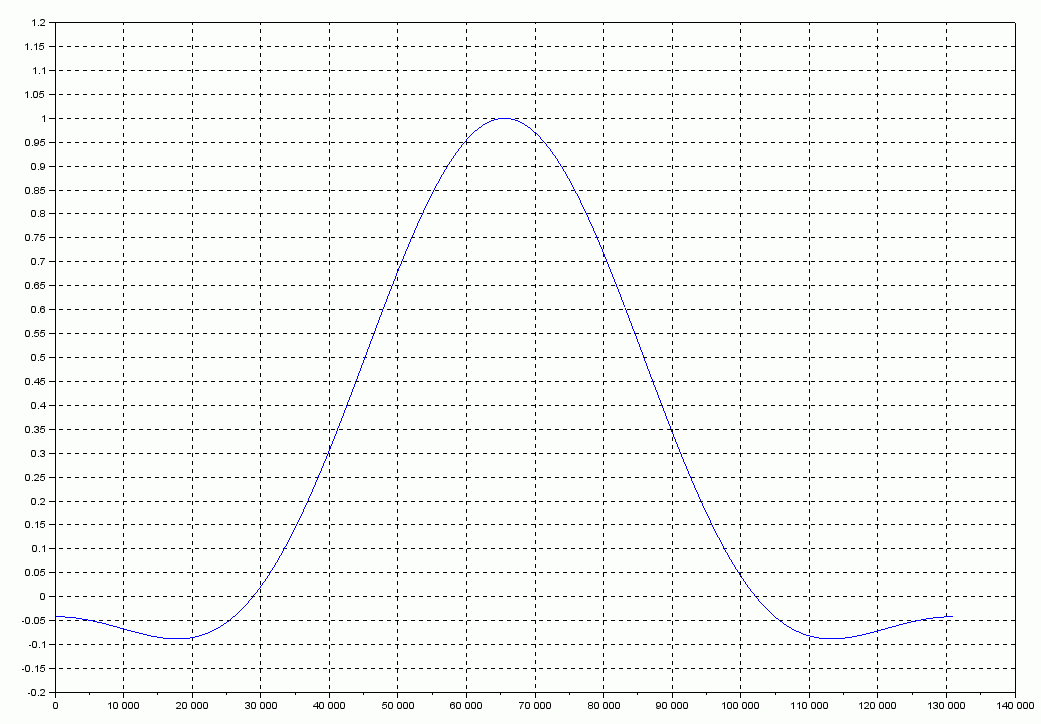
Рисунок 6 Весовая функция FlatTop

Нормирующий коэффициент для отсчётов:

-->K=1/(sum(abs(H))/(2^17));

Перемножаем два вектора (отсчётов и оконной функции) с учётом нормирующего коэффициента:

-->yw=y(1:2^17).*H; % поэлементно перемножаем
-->plot(yw);
-->xgrid(100);

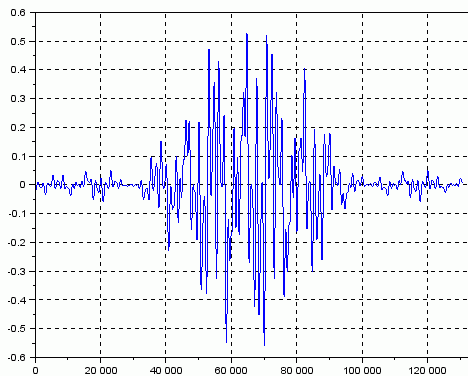
Рисунок 7 “Взвешенный” окном сигнал

Нормируем:

->yw=yw*K;

Вычисляем спектр:

-->YW=fft(yw(1: 131072));
-->plot(abs(YW));

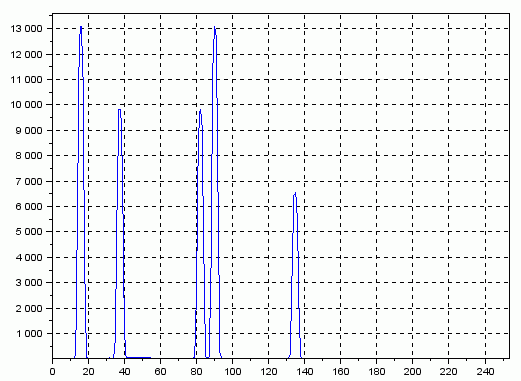
Рисунок 8 АЧС для отсчётов, внизу частоты (Гц.)

После устранения “эффекта частокола” видно, что некоторые частотные составляющие имеют, на самом деле, приблизительно равные амплитуды.

АЧС эквивалентен удвоенной амплитуде части положительных частот (слева от Fs/2).

Поэтому, чтобы получить нормировку по амплитуде в единицах квантования АЦП, нужно умножить их на 

K₂ = 2/N ,

где N – количество элементов в выборке.

-->clf();
-->plot((2/2^17)*abs(YW));
-->xgrid(99);

 Рисунок 9. Нормированный АЧС

Удачного спектрального анализа Вам!